STAT Online homework help
Worksheet Difficulty: 1Easy Learning Objective: 0806 Know when to use Students t instead of z to estimate μ.
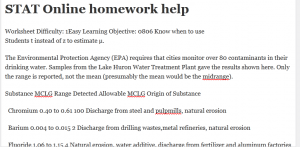
The Environmental Protection Agency (EPA) requires that cities monitor over 80 contaminants in their drinking water. Samples from the Lake Huron Water Treatment Plant gave the results shown here. Only the range is reported, not the mean (presumably the mean would be the midrange).
Substance MCLG Range Detected Allowable MCLG Origin of Substance
Chromium 0.40 to 0.61 100 Discharge from steel and pulpmills, natural erosion
Barium 0.004 to 0.015 2 Discharge from drilling wastes,metal refineries, natural erosion
Fluoride 1.06 to 1.15 4 Natural erosion, water additive, discharge from fertilizer and aluminum factories
MCLG = Maximum contaminant level goal
For each substance, estimate the standard deviation σ by assuming Uniform Distribution and Normal Distribution shown in Table 8.11 in Section 8.8. (Round your answers to 4 decimal places.) Uniform Distribution Normal Distribution Chromium Barium Fluoride
References
Worksheet Difficulty: 2Medium Learning Objective: 0809 Sample Size Determination for a Proportion
0.0606 0.035 0.0032 0.0018 0.026 0.015
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 2/11
4. Award: 4.16 points
5. Award: 4.16 points
(a) A poll of 2,224 likely voters was conducted on the president’s performance. Approximately what margin of error would the approval rating estimate have? (Round your answer to 4 decimal places.)
Margin of error
(b) The poll showed that 48 percent approved the president’s performance. Construct a 90 percent confidence interval for the true proportion. (Round your answers to 4 decimal places.)
The 90% confidence interval to
(c) The percentage of all voters opposed is likely to be 50 percent.
Yes, the confidence interval contains .50 No, the confidence interval does not contain .50
References
Worksheet Difficulty: 2Medium Learning Objective: 0807 Construct a 90, 95, or 99 percent confidence interval for π.
Find the interval [ ] within which 95 percent of the sample means would be expected to fall, assuming that each sample is from a normal population.
(a) μ = 159, σ = 20, n = 44. (Round your answers to 2 decimal places.)
The 95% range is from to .
(b) μ = 1,036, σ = 25, n = 6. (Round your answers to 2 decimal places.)
The 95% range is from to .
(c) μ = 44, σ = 3, n = 20. (Round your answers to 3 decimal places.)
The 95% range is from to .
References
Worksheet Learning Objective: 0803 State the Central Limit Theorem for a mean.
Difficulty: 1Easy Learning Objective: 0804 Explain how sample size affects the standard error.
The fuel economy of a 2011 Lexus RX 350 2WD 6 cylinder 3.5 L automatic 5−speed using premium fuel is a normally distributed random variable with a mean of μ = 26 MPG and a standard deviation of σ = 2.5
0.0205
0.423 0.458
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 3/11
6. Award: 4.16 points
MPG.
(a)What is the standard error of , the mean from a random sample of 16 fill−ups by one driver? (Round your answer to 4 decimal places.)
Standard error of
(b)Within what interval would you expect the sample mean to fall, with 90 percent probability? (Round your answers to 4 decimal places.)
The interval is from to
References
Worksheet Learning Objective: 0803 State the Central Limit Theorem for a mean.
Difficulty: 2 Medium
Learning Objective: 0804 Explain how sample size affects the standard error.
[The following information applies to the questions displayed below.] Concerns about climate change and CO2 reduction have initiated the commercial production of blends of
biodiesel (e.g., from renewable sources) and petrodiesel (from fossil fuel). Random samples of 32 blended fuels are tested in a lab to ascertain the bio/total carbon ratio.
(a) If the true mean is 0.913 with a standard deviation of 0.004, within what interval will 98 percent of the sample means fall? (Round your answers to 4 decimal places.)
The interval is from to
Hint #1
References
Worksheet Learning Objective: 0803 State the Central Limit Theorem for a mean.
Difficulty: 2 Medium
Learning Objective: 0804 Explain how sample size affects the standard error.
0.625
24.972 27.028
Hints
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 4/11
7. Award: 4.16 points
8. Award: 4.16 points
(b) If the true mean is 0.913 with a standard deviation of 0.004, what is the sampling distribution of ?
rev: 09_10_2012, 06_05_2013_QC_31318
Exactly Normal with μ = 0.913 and σ = 0.004.
Approximately Normal with μ = 0.913 and σ = 0.004.
Exactly Normal with μ = 0.913 and
Approximately Normal with μ = 0.913 and
Hint #1
References
Multiple Choice Learning Objective: 08-03 State the Central Limit Theorem for a mean.
Difficulty: 2-Medium Learning Objective: 08-04 Explain how sample size affects the standard error.
(c) Which theorem did you use to answer part (b)?
Pythagorean Theorem
Law of Large Numbers
Chebyshev’s Theorem
Central Limit Theorem
Hint #1
References
Multiple Choice Learning Objective: 08-03 State the Central Limit Theorem for a mean.
Hints
Hints
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 5/11
9. Award: 4.16 points
10. Award: 4.16 points
11. Award: 4.16 points
Difficulty: 2-Medium Learning Objective: 08-04 Explain how sample size affects the standard error.
[The following information applies to the questions displayed below.] Use the sample information = 34, σ = 4, n = 10 to calculate the following confidence intervals for μ assuming the sample is from a normal population.
(a) 90 percent confidence. (Round your answers to 4 decimal places.)
The 90 percent confidence interval is from to
References
Worksheet Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
(b) 95 percent confidence. (Round your answers to 4 decimal places.)
The 95 percent confidence interval is from to
References
Worksheet Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
(c) 99 percent confidence. (Round your answers to 4 decimal places.)
The 99 percent confidence interval is from to
References
Worksheet Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 6/11
12. Award: 4.16 points
13. Award: 4.16 points
14. Award: 4.16 points
(d) Describe how the intervals change as you increase the confidence level.
The interval gets narrower as the confidence level increases.
The interval gets wider as the confidence level increases.
The interval stays the same as the confidence level increases.
The interval gets wider as the confidence level decreases.
References
Multiple Choice Difficulty: 1-Easy Learning Objective: 08-05 Construct a 90, 95, or 99 percent confidence interval for μ.
[The following information applies to the questions displayed below.]
A random sample of 135 items is drawn from a population whose standard deviation is known to be σ = 60. The sample mean is = 870.
(a) Construct an interval estimate for μ with 98 percent confidence. (Round your answers to 4 decimal places.)
The 98 percent confidence interval is from to .
rev: 04_04_2014_QC_47908
References
Worksheet Learning Objective: 0804 Explain how sample size affects the standard error.
Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 7/11
15. Award: 4.16 points
16. Award: 4.16 points
(b)Construct an interval estimate for μ with 98 percent confidence, assuming that σ = 120. (Round your answers to 4 decimal places.)
The 98 percent confidence interval is from to .
References
Worksheet Learning Objective: 0804 Explain how sample size affects the standard error.
Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
(c) Construct an interval estimate for μ with 98 percent confidence, assuming that σ = 240. (Round your answers to 4 decimal places.)
The 98 percent confidence interval is from to .
References
Worksheet Learning Objective: 0804 Explain how sample size affects the standard error.
Difficulty: 1Easy Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
(d) Describe how the confidence interval changes as σ increases.
The interval gets narrower as σ increases.
The interval stays the same as σ increases.
The interval gets wider as σ decreases.
The interval gets wider as σ increases.
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 8/11
17. Award: 4.16 points
18. Award: 4.16 points
References
Multiple Choice Learning Objective: 08-04 Explain how sample size affects the standard error.
Difficulty: 1-Easy Learning Objective: 08-05 Construct a 90, 95, or 99 percent confidence interval for μ.
The Ball Corporation’s beverage can manufacturing plant in Fort Atkinson, Wisconsin, uses a metal supplier that provides metal with a known thickness standard deviation σ = 0.000742 mm. If a random sample of 48 sheets of metal resulted in an = 0.2731 mm.
Calculate the 95 percent confidence interval for the true mean metal thickness. (Round your answers to 4 decimal places.)
The 95% confidence interval to
References
Worksheet Learning Objective: 0804 Explain how sample size affects the standard error.
Difficulty: 2 Medium
Learning Objective: 0805 Construct a 90, 95, or 99 percent confidence interval for μ.
Find a confidence interval for μ assuming that each sample is from a normal population. (Round the value of t to 3 decimal places and your final answers to 2 decimal places.) (a) = 28, s = 5, n = 6, 90 percent confidence.
The 90% confidence interval is to (b) = 49, s = 4, n = 19, 99 percent confidence.
The 99% confidence interval is to (c) = 126, s = 15, n = 21, 95 percent confidence.
The 95% confidence interval is to
Hint #1
Hints
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 9/11
19. Award: 4.16 points
20. Award: 4.16 points
References
Worksheet Difficulty: 1Easy Learning Objective: 0806 Know when to use Student’s t instead of z to estimate μ.
A random sample of 16 pharmacy customers showed the waiting times below (in minutes).
15 12 17 17 14 16 17 22 19 23 14 25 17 12 17 18
Click here for the Excel Data File
Find a 90 percent confidence interval for μ, assuming that the sample is from a normal population. (Round the value of t to 3 decimal places. Round your final answers to 3 decimal places.)
The 90% confidence interval to
References
Worksheet Difficulty: 2Medium Learning Objective: 0806 Know when to use Student’s t instead of z to estimate μ.
A random sample of 10 shipments of stickon labels showed the following order sizes.
22,485 56,758 59,762 17,671 16,301 12,262 48,307 51,196 47,326 31,943
Click here for the Excel Data File
(a) Construct a 95 percent confidence interval for the true mean order size. (Round your answers to the nearest whole number.)
The 95 percent confidence interval to
(b) The confidence interval can be made narrower by
decreasing the sample size or increasing the confidence level. decreasing the sample size or decreasing the confidence level. increasing the sample size or decreasing the confidence level. increasing the sample size or increasing the confidence level.
References
Worksheet Difficulty: 2Medium Learning Objective: 0806 Know when to use Student’s t instead of z to estimate μ.
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 10/11
21. Award: 4.16 points
22. Award: 4.16 points
23. Award: 4.16 points
Calculate the standard error. May normality be assumed? (Round your answers to 4 decimal places.)
Standard Error Normality (a) n = 29, π = 0.20 (Click to select) (b) n = 45, π = 0.18 (Click to select) (c) n = 90, π = 0.57 (Click to select) (d) n = 442, π = 0.001 (Click to select)
References
Worksheet Difficulty: 1Easy Learning Objective: 0807 Construct a 90, 95, or 99 percent confidence interval for π.
Find the margin of error for a poll, assuming that 95% confidence and = 0.1.
(a) n = 40 (Round your answer to 4 decimal places.)
Margin of error
(b) n = 160 (Round your answer to 4 decimal places.)
Margin of error
(c) n = 400 (Round your answer to 4 decimal places.)
Margin of error
(d) n = 1,600 (Round your answer to 4 decimal places.)
Margin of error
References
Worksheet Difficulty: 1Easy Learning Objective: 0807 Construct a 90, 95, or 99 percent confidence interval for π.
Of 54 bank customers depositing a check, 23 received some cash back.
(a) Construct a 90 percent confidence interval for the proportion of all depositors who ask for cash back. (Round your answers to 4 decimal places.)
The 90% confidence interval is from to
(b)May normality of p be assumed?
11/12/2015 Assignment Print View
http://ezto.mheducation.com/hm.tpx 11/11
24. Award: 4.32 points
Yes No
References
Worksheet Difficulty: 2Medium Learning Objective: 0807 Construct a 90, 95, or 99 percent confidence interval for π.
The city fuel economy of a 2009 Toyota 4Runner 2WD 6 cylinder 4 L automatic 5speed using regular gas is a normally distributed random variable with a range 16 MPG to 21 MPG.
(a) Estimate the standard deviation using Method 3 (the Empirical Rule for a normal distribution). (Round your answer to 4 decimal places.)
Standard deviation
(b)What sample size is needed to estimate the mean with 90 percent confidence and an error of ± 0.25 MPG? (Enter your answer as a whole number (no decimals). Use a zvalue taken to three decimal places in your calculations.)